
Betreuer: Herr Daniel Schmitt
Implementieren und Visualisieren Sie einen randomisiert inkrementellen Algorithmus zur Berechnung der Delaunay-Triangulierung. Der Algorithmus ist in „Incremental Delaunay Triangulation“ von Dani Lischinski beschrieben. Statt der dort verwendeten Datenstruktur benutzen Sie den Leda Graphen.
Weiter zu beachten:
Gegeben ist eine Punktmenge L = {l1 ,…, ln}. Eine Delaunay-Triangulierung ist eine Triangulierung der konvexen Hülle der Menge L, bei der gilt: Bilden li, lj, lk ein Dreieck in dieser Triangulierung, so gibt es keinen weiteren Punkt lm aus L, der innerhalb des Kreises liegt, der durch li, lj, lk läuft. Es ergibt sich ein planarer Graph.
Initialisierung: Es wird ein Dreieck T um alle Punkte der Eingabemenge L gelegt. Dadurch wird sichergestellt, dass die Dreieckslokalisierung für jeden Punkt ausgeführt werden kann. T hat durch die Delaunay-Eigenschaft keinen Einfluß auf die entstandene Triangulierung und kann deshalb am Ende entfernt werden. Das Ergebnis ist die Triangulierung von L in G.
set<point> L; /* Eingabemenge */
Graph G; /* initial leer */
point s = init(L);
while (!L.empty()) {
point p = L.pop();
triangle D_dest = find_face(s, p);
triangulate(D_dest, p);
s = p;
}
Der Algorithmus arbeitet inkrementell, d.h. für jeden neu eingegebenen Punkt 'dest' wird die bereits vorhandene Triangulierung entsprechend erweitert.
Erster Schritt ist die Lokalisierung des Faces 'X' in G, das das Dreieck Ddest, das 'dest' enthält, repräsentiert.
Anschließend wird 'dest' als neuer Knoten in den Graphen eingefügt und für alle Dreiecke Da, die an Ddest mit einer Seite 'a' angrenzen, wird die Delaunay-Bedingung wieder hergestellt: Der Kreis um die drei Eckpunkte von Da darf den neuen Punkt 'dest' nicht enthalten, ansonsten muss anders trianguliert werden.
Source: delaunay.cpp
Der Delaunay-Graph wird mit Hilfe der GRAPH-Datenstruktur aus der LEDA-Bibliothek bidirektional aufgebaut. Die Zuordnung zu Punkten in ℚ² erfolgt mittels rat_points.
Die Punkte gibt der Benutzer via Maus in ein GeoWin ein.
LEDA stellt folgende Prädikate zur Verfügung:
| Incircle-Test | Orientation-Test | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Gegeben sind die Punkte p,q,r,s. Der Incircle-Test bestimmt, ob der Punkt p innerhalb oder außerhalb des durch q,r,s aufgespannten Kreises liegt. Das Ergebnis wird durch folgende Determinante bestimmt: det(A) =
Abhängig davon, in welcher Anordnung r, q und s zueinander liegen, liegt p außerhalb des Kreises, wenn det(A) < 0 (q, r, s im Uhrzeigersinn) oder innerhalb des Kreises im umgekehrten Fall. |
Gegeben sind Punkte q, r, s. Der Orientation-Test bestimmt, auf welcher Seite einer Gerade g durch q und r der Punkt s liegt. Dies geschieht mit folgender Determinante: det(B) =
Die LEDA-Funktion gibt |
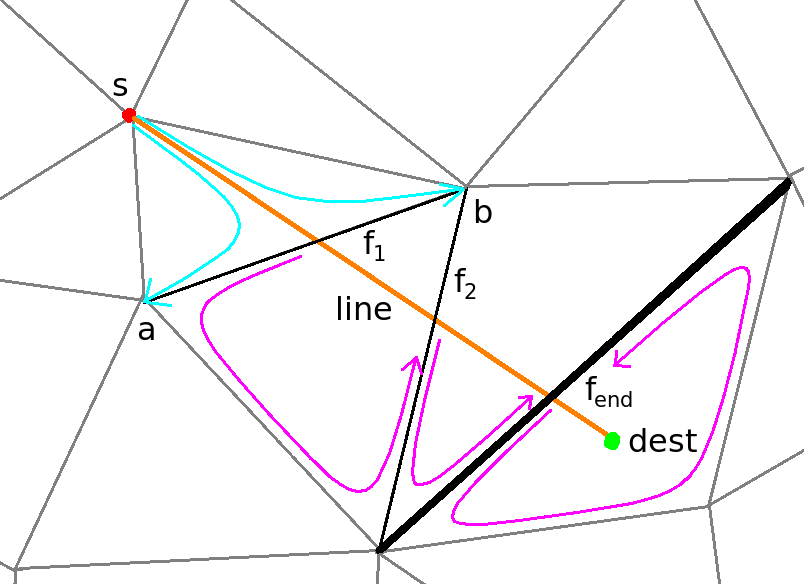 Abb. 1: Wegfindung von 's' zu Ddest. Variable 'f' im Code zeigt in jeder
Abb. 1: Wegfindung von 's' zu Ddest. Variable 'f' im Code zeigt in jeder find_next-Iteration auf eine
Kante fi. Die violetten Pfeile stellen den Pfad dar, der pro Iteration überprüft wird, bis folgendes fi+1
gefunden wird.
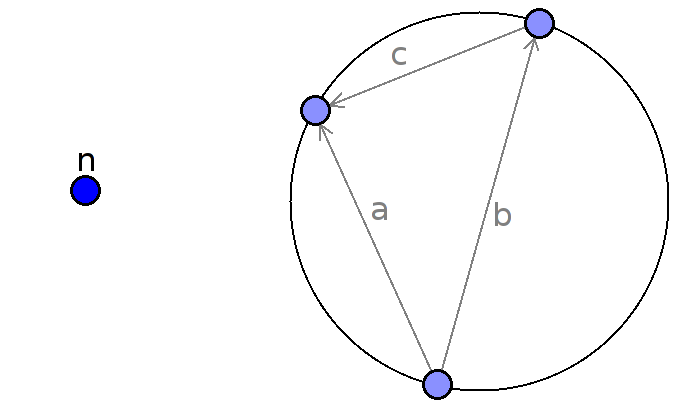 Abb. 2: Face 'X' mitsamt Bezeichnung seiner Kanten.
Abb. 2: Face 'X' mitsamt Bezeichnung seiner Kanten.
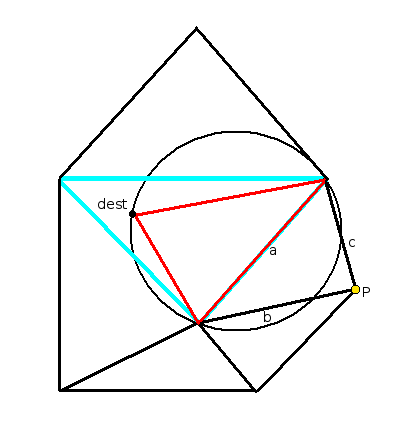 Abb. 3: Innerhalb des türkisgefärbten Dreiecks Ddest liegt der neue Punkt 'dest'. Der Kreis, der durch
das rote Dreieck definiert ist, verletzt die Delaunay-Bedingung nicht, da der Punkt P
nicht in ihm enthalten ist.
Abb. 3: Innerhalb des türkisgefärbten Dreiecks Ddest liegt der neue Punkt 'dest'. Der Kreis, der durch
das rote Dreieck definiert ist, verletzt die Delaunay-Bedingung nicht, da der Punkt P
nicht in ihm enthalten ist.
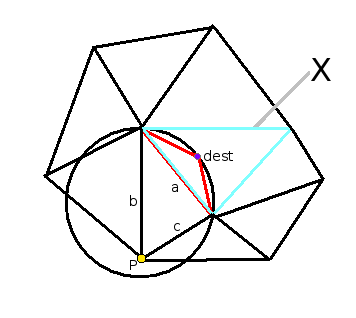 Abb. 4: Der Kreis, der durch
das rote Dreieck definiert ist, verletzt die Delaunay-Bedingung, da der Punkt P
im Inneren des Kreises liegt.
Abb. 4: Der Kreis, der durch
das rote Dreieck definiert ist, verletzt die Delaunay-Bedingung, da der Punkt P
im Inneren des Kreises liegt.
Alle vom Benutzer eingegebenen Punkte werden in einer Liste 'points' gespeichert. Das äußere Dreieck ist immer groß genug, um das kleinste Rechteck, das die Punktemenge enthält, einzuschließen. Da das Dreieck anhand der maximalen und minimalen x-/y-Koordinaten der Eingabemenge berechnet wird, ist es immer gleichschenklig mit der Basis entlang der X-Achse.
Besteht die Eingabe aus nur einem Punkt, wird ein neues Dreieck erstellt und mit seinen Eckpunkten als Knoten in den Graphen eingefügt. Als Startpunkt 's' für eine darauf folgende Eingabe wird die Spitze des Dreiecks verwendet.
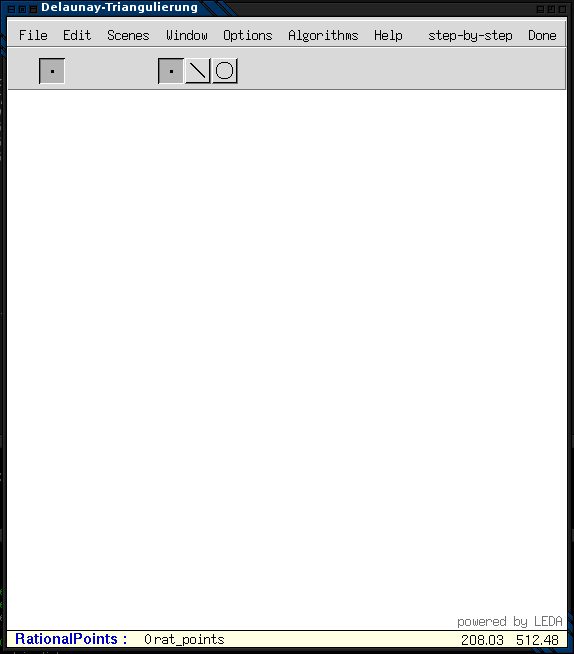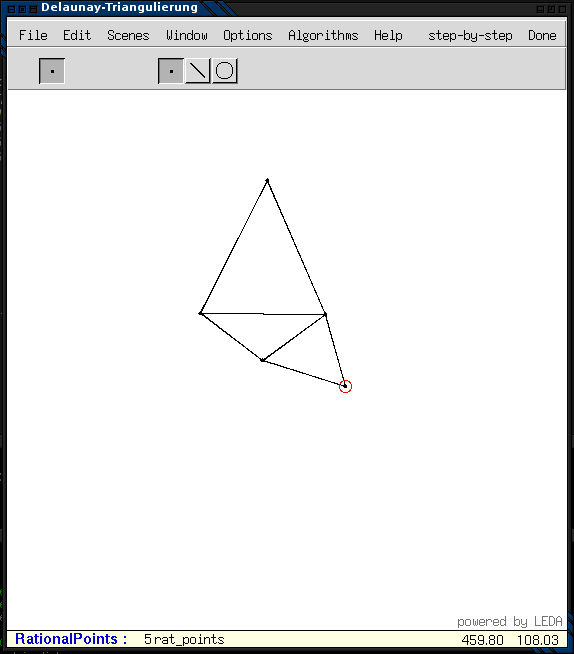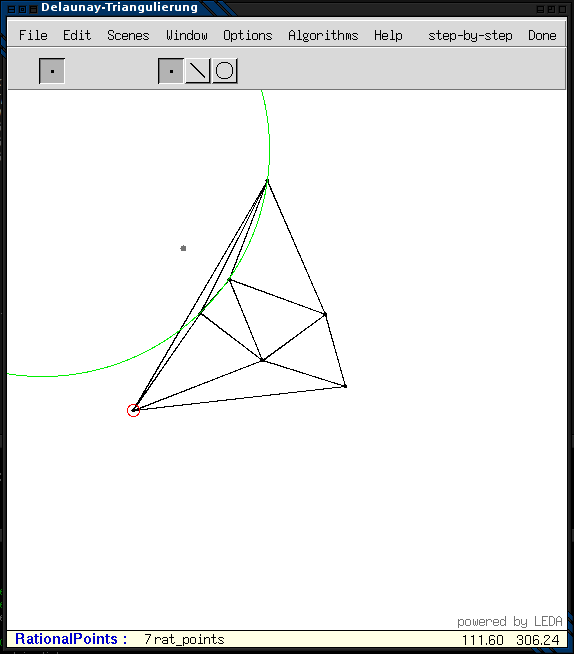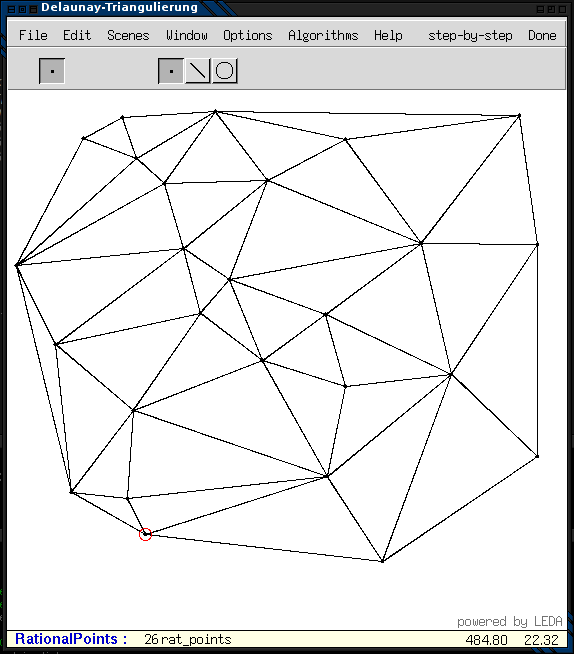
Wird nun ein neuer Punkt eingefügt, so wird die Ausdehnung der Menge neu erfasst und das bestehende Dreieck entsprechend vergrößert.
find_next:
e = f;
while ((e = G.cyclic_adj_succ(G.reversal(e))) != f) {
if (intersects(G[G.source(e)], G[G.target(e)],
G[s], dest)) {
f = G.reversal(e);
goto find_next;
}
}
return f;
Es wird die Strecke vom zuletzt eingefügten Punkt 's' zum neu eingefügten Punkt 'dest' gebildet. Mit Hilfe von zwei Orientation-Tests (Abb. 1: Pfeile in Cyan) wird das Startdreieck 'bsa' bestimmt. ‚dest’ liegt darin bzw. 'line' läuft hindurch.
Die Methode sucht nun iterativ nach dem Face in G, das 'dest' enthält. f1 wird als die zu ab gehörige Kante in G definiert. In Iteration i wird im aktuellen Face nach einer Kante fi+1 gesucht, die 'line' schneidet. Es wird mit dem dort angrenzenden Face fortgefahren. Da in jedem Face höchstens zwei Seiten von der Strecke geschnitten werden, ist der Weg eindeutig bestimmt.
Dies wird solange wiederholt bis bei einem Face von fi aus kein fi+1 mehr gefunden wird. fend ist
dann reversal(fi). Das zum Face gehörige Dreieck Ddest enthält ‚dest’. Zurückgegeben wird die Kante
fend. Der Aufbau der Suche garantiert, dass der gesuchte Punkt links der Kante liegt.
while (!check.empty()) {
a = check.pop_back();
b = G.cyclic_adj_pred(a);
c = G.cyclic_adj_pred(G.reversal(b));
bool flip;
if (orientation(G[G.source(b)],
G[G.target(b)], G[n]) == -1 &&
orientation(G[G.source(c)],
G[G.target(c)], G[n]) == -1 &&
orientation(G[G.source(a)],
G[G.target(a)], G[n]) == 1) {
flip = false;
} else {
flip = incircle(G[G.source(a)],
G[G.target(a)],
G[G.target(b)],
G[n]);
}
if (flip) {
G.del_edge(a);
check.push_back(c);
check.push_back(b);
} else {
edge ra = G.reversal(a);
b = G.new_edge(n, ra, false, before);
c = G.new_edge(a, n, false, behind);
G.set_reversal(b, c);
}
}
Diese Methode fügt einen neuen Knoten 'n' mit Information 'dest' in den Graphen ein. Es wird ein Stack 'check' aufgebaut, der die Kanten beinhaltet, die noch auf die Delaunay-Bedingung überprüft werden müssen.
Jede Kante 'a' in 'check' steht für dasjenige Face 'X', das rechts von 'a' liegt. Dabei sei Da das von 'X' repräsentierte
Dreieck. Falls source(a) und target(a)
auf der konvexen Hülle liegen, so existiert 'X' nicht.
Allein mit Hilfe
des Graphs kann dieser Fall nicht
abgefragt werden, denn in beiden Fällen gibt es eine Kante 'b' als zyklischen Vorgänger von 'a'. Deshalb wird
mit Hilfe von Orientation-Tests überprüft, ob 'dest' in Da liegt.
Existiert kein 'X', so entfällt auch die Überprüfung auf seine
Delaunay-Tauglichkeit.
'check' enthält die Kanten immer entgegen des Uhrzeigersinns. Beginnend mit der zuerst eingefügten Kante 'a' wird die Delaunay-Bedingung für das jeweilige Da überprüft.
Ergibt der Incircle-Test, dass der Punkt 'dest' innerhalb des Kreises um die drei Eckpunkte von Da liegt, so ist die
Delaunay-Bedingung verletzt. Die beiden Kanten 'c' und 'b' werden auf den Stack 'check' gelegt.
Eine Kante von source(a) zu 'n' wird erst ab dem Da eingefügt, das die
Delaunay-Bedingung nicht mehr verletzt. Dadurch werden doppelte Kanten von source(a) ausgehend vermieden. Somit wird
source(a) genau dann mit 'n' verbunden, wenn auch source(a) im nächsten Schleifendurchlauf wechselt. Da die Kanten
um Ddest entgegen des Uhrzeigersinns durchlaufen werden, werden alle neuen Kanten zu 'n' auch entgegen des
Uhrzeigersinns in seine Adjazenzliste eingefügt.
Ist 'check' leer, so wurde die Delaunay-Bedingung für alle Dreiecke wieder hergestellt. Der für 'dest' neu eingefügte Knoten 'n' wird zurückgegeben, um von dieser Stelle aus mit dem Algorithmus fortzufahren, sobald ein neuer Punkt eingeben wird.
Autoren: Franz Brauße, Katrin Zimmer, Xin Zhou
Erstellt am 28.01.2009, letzte Änderung am 03.02.2009